Information Theory & Bayesian ML

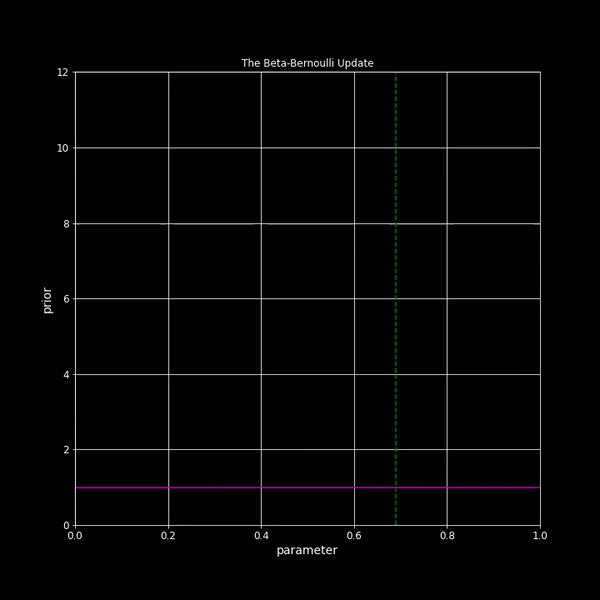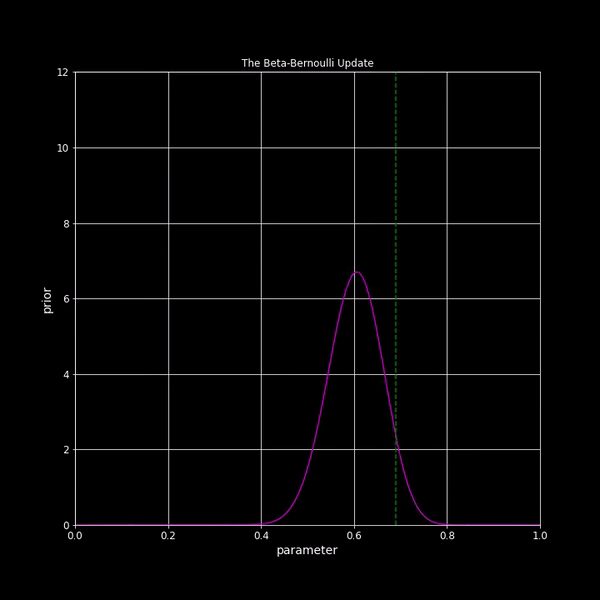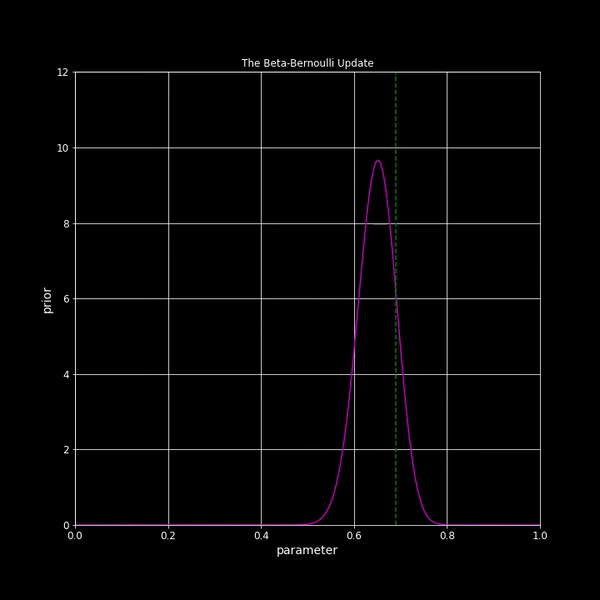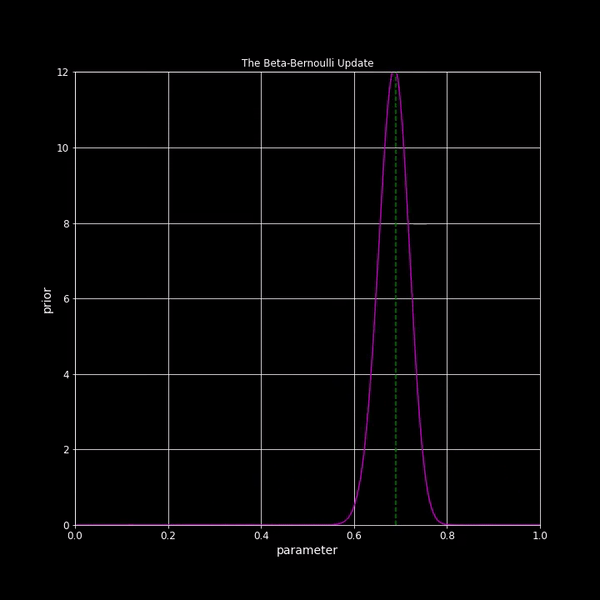Beta-Bernoulli Update

Course Information

• Lectures: MW 11:25am-12:40pm, Mann 107
• Instructor: Sid Banerjee, 229 Rhodes Hall, email
• Teaching Assistant: Spencer Peters
  

Recitation and office hours available on Piazza.

• Course Logistics:

  • Zoom: Main lecture meeting link (passwd: Shannon)
  • Piazza: All course communications via Piazza page. Please join immediately if not automatically added.
  • CMSx: Homework submissions must be done electronically via CMSx.
    

Textbooks

We will mainly follow two textbooks

• Information Theory, Inference, and Learning Algorithms by David Mackay

• Pattern Recognition and Machine Learning by Chris Bishop

Both these books have free pdfs available on their websites, and are both excellent resources! We will cover a selection of chapters from each, as well as some additional topics (depending on time/interest).

Lecture Notes

• Lecture 1: Introduction

  – [slides]

  – [annotated] [lecture recording]
  – Who was Claude Shannon: short documentary and longer movie

• Lecture 2: Probability review

  – [slides]

  – [annotated] [lecture recording]
  – Demo of Bertrand’s paradox: [Jupyter notebook]
  – Intuitive demos: conditional probability, Bayes theorem, likelihood ratios

• Lecture 3: Measuring information

  – [slides]

  – [annotated] [lecture recording]
  – Some videos: Shannon’s formula of entropy, Documentary on “Order and Disorder” (traces entropy from physics to computer science to information theory)

• Lecture 4: Data compression 1: Lossy compression

  – [slides]

  – [annotated] [lecture recording]
  – Video series on data compression (by Google developers): Compressor Head

• Lecture 5: Data compression 2: Typicality and lossless compression

  – [annotated] [lecture recording]
  – Kraft-Mcmillan inequality (check out the proof of the general case; I personally find it quite unique and surprising!)

• Lecture 6: Data compression 3: The entropy lower bound, and symbol codes

  – [annotated] [lecture recording]
  – Huffman codes
  – A very nice visual explanation of information and symbol codes: Visual information theory

• Lecture 7: Data compression 4: Stream codes

  – [annotated] [lecture recording]
  – Using arithmetic codes for predictive typing: Dasher project, short demo, talk by David Mackay

• Lecture 8: Dependent random variables and mutual information

  – [slides]

  – [annotated] [lecture recording]

• Lecture 9: The channel coding theorem

  – [annotated] [lecture recording]

• Lecture 10: Intro to Bayesian statistics

  – [slides]

  – [annotated] [lecture recording]

• Lecture 11: The Beta-Bernoulli model

  – [annotated] [lecture recording]

• Lecture 12: Bayesian Networks

  – [slides]

  – Guest lecture by Spencer Peters

  – [annotated] [lecture recording]

• Lecture 13: The Dirichlet model and Naive Bayes

  – [annotated] [lecture recording]

• Lecture 14: The Gaussian-Gaussian and Gaussian-Gamma models

  – [annotated] [lecture recording]

• Lecture 15: Bayesian Linear Regression

  – [slides]
  – Bayesian regression notebook: [Jupyter notebook]

  – [annotated] [lecture recording]

• Lecture 16: Bayesian Model Selection

  – [annotated] [lecture recording]

• Lecture 17: Gaussian Processes

  – [slides]

  – [annotated] [lecture recording]

• Lecture 18: Gaussian Process Regression

  – GP regression notebook: [Jupyter notebook]

  – [annotated] [lecture recording]

• Lecture 19: Hyperparameter Tuning via Empirical Bayes, GP Classification

  – [annotated] [lecture recording]

• Lecture 20: GP classification via the Laplace Approximation

  – [annotated] [lecture recording]

• Lecture 21: Laplace Approximation, and Intro to Monte Carlo methods

  – GP classification notebook: [Jupyter notebook]

  – [annotated] [lecture recording]

• Lecture 22: Importance Sampling and Intro to Markov Chains

  – [annotated] [lecture recording]

• Lecture 23: Markov Chain Monte Carlo

  – MCMC notebook: [Jupyter notebook]

  – [annotated] [lecture recording]

• Lecture 24: Mixture Models and the EM Algorithm

  – Gaussian Mixture Models notebook: [Jupyter notebook]

  – [annotated] [lecture recording]

Assignments

• Assignment 1: Problems

• Assignment 2: Problems